|
|
|

A number is said to be squarefree (or sometimes Quadratfrei; Shanks 1993) if its Prime decomposition contains no repeated factors. All Primes are therefore trivially squarefree. The squarefree numbers are 1, 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, ... (Sloane's A005117). The Squareful numbers (i.e., those that contain at least one square) are 4, 8, 9, 12, 16, 18, 20, 24, 25, ... (Sloane's A013929).
The asymptotic number ![]() of squarefree numbers
of squarefree numbers ![]() is given by
is given by
| (1) |
The Möbius Function is given by
 |
(2) |
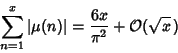 |
(3) |
There is no known polynomial-time algorithm for recognizing squarefree Integers or for computing the
squarefree part of an Integer. In fact, this problem may be no easier than the general problem of integer factorization
(obviously, if an integer ![]() can be factored completely,
can be factored completely, ![]() is squarefree Iff it contains no duplicated factors).
This problem is an important unsolved problem in Number Theory because computing the Ring of integers of an
algebraic number field is reducible to computing the squarefree part of an Integer (Lenstra 1992, Pohst and Zassenhaus
1997). The Mathematica
is squarefree Iff it contains no duplicated factors).
This problem is an important unsolved problem in Number Theory because computing the Ring of integers of an
algebraic number field is reducible to computing the squarefree part of an Integer (Lenstra 1992, Pohst and Zassenhaus
1997). The Mathematica
![]() (Wolfram Research, Champaign, IL) function NumberTheory`NumberTheoryFunctions`SquareFreeQ[n] determines whether a number is squarefree.
(Wolfram Research, Champaign, IL) function NumberTheory`NumberTheoryFunctions`SquareFreeQ[n] determines whether a number is squarefree.
All numbers less than
![]() in Sylvester's
Sequence are squarefree, and no Squareful numbers in this sequence are known (Vardi 1991). Every Carmichael
Number is squarefree. The Binomial Coefficients
in Sylvester's
Sequence are squarefree, and no Squareful numbers in this sequence are known (Vardi 1991). Every Carmichael
Number is squarefree. The Binomial Coefficients
![]() are squarefree only for
are squarefree only for
![]() , 3, 4, 6, 9, 10, 12, 36, ..., with no others less than
, 3, 4, 6, 9, 10, 12, 36, ..., with no others less than ![]() . The Central Binomial Coefficients are Squarefree only for
. The Central Binomial Coefficients are Squarefree only for ![]() , 2, 3, 4, 5, 7, 8, 11, 17, 19, 23, 71, ... (Sloane's A046098), with
no others less than 1500.
, 2, 3, 4, 5, 7, 8, 11, 17, 19, 23, 71, ... (Sloane's A046098), with
no others less than 1500.
See also Binomial Coefficient, Biquadratefree, Composite Number, Cubefree, Erdös Squarefree Conjecture, Fibonacci Number, Korselt's Criterion, Möbius Function, Prime Number, Riemann Zeta Function, Sárközy's Theorem, Square Number, Squareful, Sylvester's Sequence
References
Bellman, R. and Shapiro, H. N. ``The Distribution of Squarefree Integers in Small Intervals.'' Duke Math. J. 21, 629-637, 1954.
Hardy, G. H. and Wright, E. M. ``The Number of Squarefree Numbers.'' §18.6 in
An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 269-270, 1979.
Lenstra, H. W. Jr. ``Algorithms in Algebraic Number Theory.'' Bull. Amer. Math. Soc. 26, 211-244, 1992.
Pohst, M. and Zassenhaus, H. Algorithmic Algebraic Number Theory.
Cambridge, England: Cambridge University Press, p. 429, 1997.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 114, 1993.
Sloane, N. J. A.
A013929,
A046098, and
A005117/M0617
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Vardi, I. ``Are All Euclid Numbers Squarefree?'' §5.1 in
Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 7-8, 82-85, and 223-224, 1991.
|
|
|
© 1996-9 Eric W. Weisstein