|
|
|
A sum is the result of an Addition. For example, adding 1, 2, 3, and 4 gives the sum 10, written
| (1) |
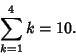 |
(2) |
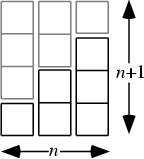
A simple graphical proof of the sum
![]() can also be given. Construct a sequence of stacks of boxes, each
1 unit across and
can also be given. Construct a sequence of stacks of boxes, each
1 unit across and ![]() units high, where
units high, where ![]() , 2, ...,
, 2, ..., ![]() . Now add a rotated copy on top, as in the above figure. Note
that the resulting figure has Width
. Now add a rotated copy on top, as in the above figure. Note
that the resulting figure has Width ![]() and Height
and Height ![]() , and so has Area
, and so has Area ![]() . The
desired sum is half this, so the Area of the boxes in the sum is
. The
desired sum is half this, so the Area of the boxes in the sum is ![]() . Since the boxes are of unit width, this
is also the value of the sum.
. Since the boxes are of unit width, this
is also the value of the sum.
The sum can also be computed using the first Euler-Maclaurin Integration Formula
![\begin{displaymath}
\sum_{k=1}^n f(k) = \int_1^n f(x)\,dx+{\textstyle{1\over 2}}...
...\over 2}}f(n)+{\textstyle{1\over 2!}} B_2 [f'(n)-f'(1)]+\ldots
\end{displaymath}](s3_1480.gif) |
(3) |
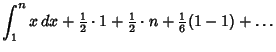 |
|||
| (4) |
The general finite sum of integral Powers can be given by the expression
![\begin{displaymath}
\sum_{k=1}^n k^p = {(B+n+1)^{[p+1]}-B^{[p+1]}\over p+1},
\end{displaymath}](s3_1485.gif) |
(5) |
An analytic solution for a sum of Powers of integers is
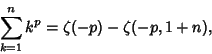 |
(6) |
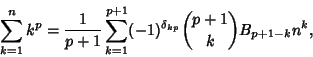 |
(7) |
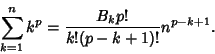 |
(8) |
| (9) | |||
| (10) | |||
| (11) | |||
| (12) | |||
| (13) | |||
| (14) | |||
| (15) | |||
| (16) | |||
| (17) | |||
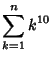 |
(18) |
|
|
(19) |
|
|
(20) |
|
|
(21) |
|
|
(22) |
|
|
(23) |
|
|
(24) |
|
|
(25) |
|
|
(26) |
|
|
(27) |
|
|
|
|
|
(28) |
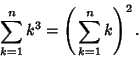 |
(29) |
Sums of the following type can also be done analytically.
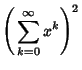 |
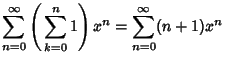 |
(30) | |
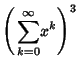 |
 |
||
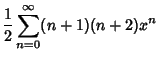 |
(31) | ||
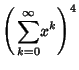 |
![$\displaystyle \sum_{n=0}^\infty \left[{\,\sum_{k=0}^n {\textstyle{1\over 2}}(k+1)(k+2)}\right]x^n$](s3_1534.gif) |
||
 |
|||
![$\displaystyle {1\over 2} \sum_{n=0}^\infty [{\textstyle{1\over 6}} n(n+1)(2n+1)+3 {\textstyle{1\over 2}}n(n+1)+2(n+1)]x^n$](s3_1536.gif) |
|||
![$\displaystyle {1\over 12} \sum_{n=0}^\infty (n+1)[n(2n+1)+9n+12]x^n$](s3_1537.gif) |
|||
 |
|||
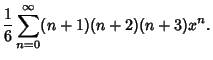 |
(32) |
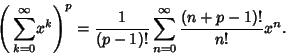 |
(33) |
Other analytic sums include
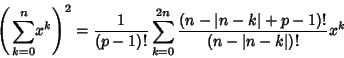 |
(34) |
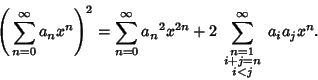 |
(35) |
| (36) |
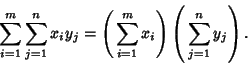 |
(37) |
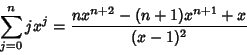 |
(38) |
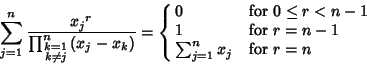 |
(39) |
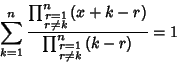 |
(40) |
![\begin{displaymath}
(n+1)\sum_{m=1}^n m^k =\sum_{m=1}^n \left[{m^{k+1}+\sum_{p=1}^n\left({\sum_{m=1}^p m^k}\right)}\right].
\end{displaymath}](s3_1551.gif) |
(41) |
To minimize the sum of a set of squares of numbers ![]() about a given number
about a given number ![]()
| (42) |
| (43) |
| (44) |
See also Arithmetic Series, Bernoulli Number, Clark's Triangle, Convergence Improvement, Dedekind Sum, Double Sum, Euler Sum, Factorial Sum, Faulhaber's Formula, Gabriel's Staircase, Gaussian Sum, Geometric Series, Gosper's Method, Hurwitz Zeta Function, Infinite Product, Kloosterman's Sum, Legendre Sum, Lerch Transcendent, Pascal's Triangle, Product, Ramanujan's Sum, Riemann Zeta Function, Whitney Sum
References
Boyer, C. B. ``Pascal's Formula for the Sums of the Powers of the Integers.'' Scripta Math. 9, 237-244, 1943.
Courant, R. and Robbins, H. ``The Sum of the First
Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A. K. Peters, 1996.
![]() Squares.'' §1.4 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 14-15, 1996.
Squares.'' §1.4 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 14-15, 1996.
|
|
|
© 1996-9 Eric W. Weisstein