|
|
|
The derivative of a Function represents an infinitesimal change in the function with respect to whatever parameters it
may have. The ``simple'' derivative of a function ![]() with respect to
with respect to ![]() is denoted either
is denoted either ![]() or
or ![]() (and
often written in-line as
(and
often written in-line as ![]() ). When derivatives are taken with respect to time, they are often denoted using
Newton's
). When derivatives are taken with respect to time, they are often denoted using
Newton's ![]() Fluxion notation,
Fluxion notation,
![]() . The derivative of a function
. The derivative of a function ![]() with
respect to the variable
with
respect to the variable ![]() is defined as
is defined as
| (1) |
A 3-D generalization of the derivative to an arbitrary direction is known as the Directional Derivative. In general, derivatives are mathematical objects which exist between smooth functions on manifolds. In this formalism, derivatives are usually assembled into ``Tangent Maps.''
Simple derivatives of some simple functions follow.
|
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
(5) |
|
|
(6) |
|
|
(7) |
|
|
(8) |
|
|
(9) |
|
|
(10) |
|
|
(11) |
|
|
(12) |
|
|
(13) |
|
|
(14) |
|
|
(15) |
|
|
(16) |
|
|
(17) |
|
|
(18) |
|
|
(19) |
|
|
(20) |
|
|
(21) |
|
|
(22) |
|
|
(23) |
|
|
(24) |
|
|
(25) |
|
|
(26) |
Derivatives of sums are equal to the sum of derivatives so that
| (27) |
| (28) |
| (29) |
| (30) |
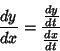 |
(31) |
| (32) |
| (33) |
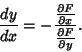 |
(34) |
A vector derivative of a vector function
![\begin{displaymath}
{\bf X}(t) \equiv\left[{\matrix{x_1(t)\cr x_2(t)\cr \vdots\cr x_k(t)\cr}}\right]
\end{displaymath}](d1_583.gif) |
(35) |
![\begin{displaymath}
{d{\bf X}\over dt} = \left[{\matrix{{dx_1\over dt}\cr {dx_2\over dt}\cr \vdots\cr {dx_k\over dt}\cr}}\right].
\end{displaymath}](d1_584.gif) |
(36) |
See also Blancmange Function, Carathéodory Derivative, Comma Derivative, Convective Derivative, Covariant Derivative, Directional Derivative, Euler-Lagrange Derivative, Fluxion, Fractional Calculus, Fréchet Derivative, Lagrangian Derivative, Lie Derivative, Power Rule, Schwarzian Derivative, Semicolon Derivative, Weierstraß Function
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 11, 1972.
Anton, H. Calculus with Analytic Geometry, 5th ed. New York: Wiley, 1987.
Beyer, W. H. ``Derivatives.'' CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL:
CRC Press, pp. 229-232, 1987.
|
|
|
© 1996-9 Eric W. Weisstein