Conical Function

Functions which can be expressed in terms of Legendre Functions of the First and Second Kinds. See Abramowitz and Stegun (1972, p. 337).

$$P^\mu_{-1/2+ip}(\cos\theta) = 1+{4p^2+1^2\over 2^2} \sin^2({\textstyle{1\over 2}}\theta)$$

$$\phantom{=} + {(4p^2+1^2)(4p^2+3^2)\over 2^24^2}\sin^4({\textstyle{1\over 2}}\theta)+\ldots$$

$$= {2\over\pi} \int_0^\theta {\cosh(pt)\,dt\over \sqrt{2(\cos t-\cos\theta)}}$$

$$Q^\mu_{-1/2\mp ip}(\cos\theta) = \pm i\sinh(p\pi)\int_0^\infty {\cos(pt)\,dt\over\sqrt{2(\cosh t+\cos \theta)}}$$

$$\phantom{=} + \int_0^\infty {\cosh(pt)\,dt\over \sqrt{2(\cos t-\cos\theta)}}.$$

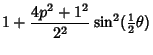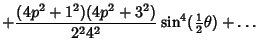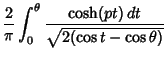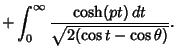See also Toroidal Function

References

Abramowitz, M. and Stegun, C. A. (Eds.). ``Conical Functions.'' §8.12 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 337, 1972.

Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1464, 1980.