|
|
|
The complex numbers are the Field ![]() of numbers of the form
of numbers of the form ![]() , where
, where ![]() and
and ![]() are Real
Numbers and i is the Imaginary Number equal to
are Real
Numbers and i is the Imaginary Number equal to ![]() . When a single letter
. When a single letter ![]() is
used to denote a complex number, it is sometimes called an ``Affix.'' The Field of complex numbers includes
the Field of Real Numbers as a Subfield.
is
used to denote a complex number, it is sometimes called an ``Affix.'' The Field of complex numbers includes
the Field of Real Numbers as a Subfield.
Through the Euler Formula, a complex number
| (1) |
| (2) |
| (3) |
| (4) |
| (5) | |||
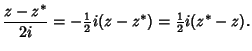 |
(6) |
![$\displaystyle \left[{x^n-{n\choose 2}x^{n-2}y^2+{n \choose 4}x^{n-4}y^4-\ldots}\right]$](c2_800.gif) |
|||
![$\displaystyle + i\left[{{n\choose 1}x^{n-1}y-{n\choose 3}x^{n-3}y^3+\ldots}\right].$](c2_801.gif) |
(7) |
| (8) | |||
| (9) | |||
| (10) | |||
| (11) |
See also Absolute Square, Argument (Complex Number), Complex Plane, i, Imaginary Number, Modulus, Phase, Phasor, Real Number, Surreal Number
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 16-17, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 353-357, 1985.
Courant, R. and Robbins, H. ``Complex Numbers.'' §2.5 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 88-103, 1996.
Morse, P. M. and Feshbach, H. ``Complex Numbers and Variables.'' §4.1 in
Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 349-356, 1953.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Complex Arithmetic.'' §5.4 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 171-172, 1992.
|
|
|
© 1996-9 Eric W. Weisstein