§ 7 Preliminary functional analysis
The
Lebesgue integral
1. Measures and Measurable Functions
[ Measurement and measurable set ] Let S be any set of bounded points in a certain interval , then the infimum of the sum of the lengths of a set of intervals covering S is called the outer measure of S, denoted as . Contains S The difference between the length of any bounded interval of and the outer measure of the complement of S (that is, the entire set of points that do not belong to S ) is called the inner measure of S, and the set S denoted by . = is called the measurable set , whose measure is denoted as .![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Let S be an unbounded point set on a straight line. If all x greater than zero is measurable , then this unbounded point set S is called measurable . In this case, the measure of the unbounded point set S is defined as![]()
![]()
This can be limited or unlimited .![]()
Every bounded open set is measurable .
The concept of measurable sets can be extended to point sets in n -dimensional spaces .
[ Almost everywhere ] A property is said to hold almost everywhere on a given interval if it holds at all points on the interval except for a set of measure zero .
[ Measurable function ] Suppose a function is defined on a measurable set S , and c is any real number . If the set formed by all points x on S is measurable, then the function is called a measurable function on S function .![]()
![]()
![]()
In this definition, the condition can be replaced by any one of , , .![]()
![]()
![]()
![]()
Any continuous function within is a measurable function within .![]()
![]()
If both are inner measurable functions, then ( a is a constant), and (the limit exists) are also inner measurable functions .![]()
![]()
![]()
![]()
![]()
![]()
2. Lebesgue integral
[ Lebesgue integral of a bounded function ] Given a bounded and measurable real function in a bounded interval , insert bisectors within the variation of ( ):![]()
![]()
![]()
![]()
![]() ( 1 )
( 1 )
And use the set formed by the point x to represent that , for each sequence of divisions ( 1 ) , at that time , the sum tends to a unique finite limit I , denoted as![]()
![]()
![]()
![]()
![]()
![]()
![]()
This quantity is called a definite integral in the Lebesgue sense, also known as a Lebesgue integral, and is said to be integrable in the interior .![]()
![]()
![]()
![]()
[ Lebesgue integral of unbounded function ] If it is an unbounded measurable function in a bounded interval , the Lebesgue integral is defined as follows:![]()
![]()
![]()
![]()
in the formula

[ Lebesgue integral over unbounded interval ] If exists for everything , then define the Lebesgue integral as follows:![]()
![]()
![]()
![]()
in the formula ![]()
It is also possible to define and .![]()
![]()
[ Lebesgue integral over a set of points ] The above definition of the Lebesgue integral of bounded and unbounded functions can be extended to the Lebesgue integral over any measurable set S. It can also be extended to the region of n -dimensional space or multiple Lebesgue integrals over measurable sets .![]()
[ Existence and Properties of Lebesgue Integrals ]
1 o Every bounded measurable set function is integrable over any bounded measurable set, and an integrable function over a measurable set S is integrable over every subset of S.
2 o The necessary and sufficient conditions for the existence of Lebesgue integrals are: the existence of Lebesgue integrals .![]()
![]()
3 o The Lebesgue integral over a set with measure equal to zero is equal to zero .
4 o Let o be a set of countable disjoint (i.e. ) measurable sets, assuming that Lebesgue integrals on and on both exist, then![]()
![]()
![]()
![]()
![]()
![]()
5 o Continuity Theorem Suppose that a positive function is measurable on a measurable set S , and for all n and all x in S , the inequality ![]()
![]()
![]()
It is established almost everywhere; and let it be established for almost all x in S , then![]()
![]()
exists, and
![]()
6 o Lebesgue's Fundamental Theorem Suppose S is a measurable set, not necessarily bounded . ![]()
like
(i) ![]() are all non-negative measurable functions on S ;
are all non-negative measurable functions on S ;
(ii)![]()
but
![]()
3. Square integrable function
[ L 2 space ] If S is a bounded measurable set, f ( x ) is a measurable function on S , integrable, and![]()
![]()
is called a function belonging to space, denoted as , or abbreviated as . In this paragraph, it is assumed that S is the interval .![]()
![]()
![]()
![]()
![]()
If , , then both are integrable; and there is![]()
![]()
![]()
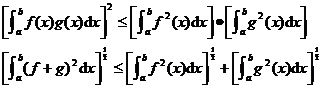
[ modulus and distance ] is set , then it is called![]()
![]()
is the norm (norm) of f .
designate _![]()
![]()
is the distance between f and g .
set rules![]()
(i) ![]() , only if it holds almost everywhere,
, only if it holds almost everywhere,![]()
![]()
(ii)![]()
(iii)![]()
[ average convergence ] if and![]()
![]()
Then the function sequence is said to be internally convergent or averagely convergent, and its limit is , denoted as![]()
![]()
![]()
Average convergence has the following properties:
1 o If , then![]()
![]()
![]()
established almost everywhere .![]()
2 o If , then![]()
![]()
![]()
3 o If , then![]()
![]()
![]()
![]() The necessary and sufficient condition for the average convergence of the point sequence in 4o is that it is a basic sequence .
The necessary and sufficient condition for the average convergence of the point sequence in 4o is that it is a basic sequence .![]()
The basic sequence is defined as follows: Let , if there is always a positive integer N for any, and for all such that![]()
![]()
![]()
![]()
is called the basic sequence in .![]()
![]()
It follows that it is a complete space (see Chapter 21, § 4 , a) .![]()
[ ![]() Divisibility of space ]
Divisibility of space ]
1 o Let , then for any , there is always a continuous function such that![]()
![]()
![]()
![]()
2 o Let , then for any polynomial , there is always a polynomial whose coefficients are rational numbers , so that![]()
![]()
![]()
![]()
Because all polynomials whose coefficients are rational numbers form a countable set and are dense everywhere in it . So 2 o is shown to be a separable space (see Chapter 21, § 3 , 3) .![]()
![]()
2. Hilbert space
[ Hilbert ( H ) space ] If each fundamental sequence in an infinite-dimensional unitary space V converges to an element in V , then V is said to be complete . A complete infinite-dimensional unitary space is called a Hilbert space, or H space for short .
A vector in an n -dimensional space is defined as the set of n numbers . Similarly , a vector in an infinite-dimensional space is defined as a function of t going from a to b .![]()
![]()
The addition and number multiplication of vectors is defined as the addition of functions and the multiplication of functions and numbers .
The formula for the inner product (quantity product) of two vectors in H space is
![]() ( 1 )
( 1 )
[ Metric of H space ] Let , then![]()
![]()
is the length of the vector . Let , the distance between the vector and![]()
![]()
![]()
![]()
![]()
This expression is called the mean square error of the function and . It is to use the mean square error as a measure of the distance between two elements in the Hilbert space H.![]()
![]()
The angle between two vectors in H space is defined as![]()
![]()
![]()
 ( 2 )
( 2 )
Because for any two functions and there are inequalities![]()
![]()
![]()
So the right-hand side of equation ( 2 ) can be viewed as the cosine of an angle .![]()
[ Orthogonal function and orthogonal function system ] If the inner product of the non-zero vector f and g , it can be known from ( 1 ) and ( 2 ) , that is . Therefore, the vector f and g are said to be orthogonal . At this time![]()
![]()
![]()
![]()
Let represent a pairwise orthogonal function, and![]()
![]()
is their sum, then the length squared is equal to the sum of the length squares .![]()
![]()
Because the length of a vector in H space is given by integral, it is similar to the quotient height theorem at this time given by the following formula:
![]()
The integrals described above, for example , refer to the Lebesgue integrals in a meaningful way .
![]()
If the function system in H space is
![]()
Any two functions in are orthogonal to each other, that is
![]()
Then this function system is called an orthogonal function system . If it also satisfies
![]()
Then this function system is called the standard orthogonal system .
[ Decomposition according to the standard orthogonal function system ] If a complete standard orthogonal function system is given in H space (that is, it is impossible to add a non-zero function that is orthogonal to all functions in the system), then all All functions can be expanded into series (average convergence) according to the functions in this system:![]()
![]()
![]()
where the function is equal to the projection of the vector on the vector in the standard orthonormal system:![]()
![]()
![]()
can prove:
![]()
Its geometric meaning is that the square of the length of a vector in H space is equal to the sum of the squares of the projection of the vector on the vector in the complete standard orthonormal system .
3. Banach space
[ Normalized Linear Space ] Let V be a linear space, for each element α in V , there is a real number corresponding to it, and it has the following properties:![]()
(i) ![]() , if and only then * , ;
, if and only then * , ;![]()
![]()
(ii) ![]() , in particular ;
, in particular ;![]()
(iii) ![]() ;
;
Then V is called a normed linear space . ![]() It is called the norm or modulus of α .
It is called the norm or modulus of α .
For a normed linear space V ,
![]()
Then V becomes a scale space . Later, when we talk about normed linear space, it is always considered to be a scale space, and its distance is expressed by formula ( 1 ) .
[ Definition and Examples of Banach Spaces ] A complete normed linear space is called a Banach space .
Example 1 ![]() is a Banach space .
is a Banach space .
Example 2 is assumed that the whole of all continuous functions defined within is denoted as C , let , belong to C , and c is any real number, define![]()
![]()
![]()
![]()
It is easy to know that C is a linear space. For C , the definition![]()
![]()
Then C is a normed linear space, which is called a space .![]()
, then the sequence of available functions converges uniformly to .![]()
![]()
![]()
![]()
It can be shown that the space is complete, so it is a Banach space .![]()
Example 3 has a bounded real number sequence
![]()
The totality of is denoted as M. Let and be two bounded sequences, a is any real number . Define sum, number multiplication and norm as follows:![]()
![]()
![]()
![]()
![]()
Then M becomes a normed linear space , which is called a convergent sequence space, abbreviated as space M. It can be proved that the space M is complete, so it is a Banach space .
[ Compactness ] Let A be a non-empty set in the scale space E , or any infinite subset of A has at least a limit point, then A is said to be a compact set .![]()
Every compact set must be bounded .
Let be a family of functions defined on the interval , if for any , there is always , when and when, the inequality![]()
![]()
![]()
![]()
![]()
![]()
![]()
If it holds for any function in A , then the family of functions A is said to be continuous in the superior degree .![]()
![]()
The Alzera-Askori theorem is assumed to be a family of continuous functions defined on , ![]()
![]()
like
(i) There is a constant M such that the functions in this family are satisfied ;![]()
(ii) A is continuous in the superior degree;![]()
Then there is a sequence of functions in A that converges uniformly above .![]()
If A is an element in space C, then the necessary and sufficient conditions for A to be compact are: All functions in A are bounded and equicontinuous .
[ Linear functional and its properties ] Consider the functional v on the Banach space V , for any point x in V , there is a real function corresponding to it, if![]()
(i) v is additive and homogeneous, that is, for any two points x and y in V and any two real numbers a , b , there is always
![]()
(ii) v is continuous, that is, when , , then it is called a linear functional on V. ![]()
![]()
![]()
Linear functionals have the following properties:
The necessary and sufficient conditions for the continuity of 1 o additive homogeneous functional are: there are constants such that![]()
![]()
![]() ( 2 ) 2 o is assumed to be a linear functional, then the infimum of the set of numbers formed by all M satisfying ( 2 ) is called the modulus or norm, denoted as ; and there is
( 2 ) 2 o is assumed to be a linear functional, then the infimum of the set of numbers formed by all M satisfying ( 2 ) is called the modulus or norm, denoted as ; and there is![]()
![]()
![]()
![]()
3 o If a linear functional sequence { } on the Banach space V exists everywhere on V , there is a constant such that![]()
![]()
![]()
![]()
This is called the Uniform Bounded Principle or the Resonance Theorem .