§ 5 Preliminary Riemannian geometry
1.
Riemann space
[ Riemann space and its metric tensor ] If there is a set of functions g ij ( x i )= g ji ( x i ) in the n -dimensional space R n , such that two adjacent points x i ,
The distance ds between x i + d x i is given by a positive definite quadratic form
d s 2
= g ij ( x )d x i d x j
Determined, then the space R n is called Riemann space, denoted as V n . The geometry in the Riemann space V n is called Riemann geometry . The quadratic type ds 2 is called the line element of V n . Differentiate into
![]()
And the arc length of any curve xi = ![]() xi ( t ) is the integral
xi ( t ) is the integral

because of the coordinate transformation
![]()
Next, ds 2 is an invariant, so
![]()
This shows that g ij ( x ) is a component of a second-order covariance tensor, which is called the metric tensor or fundamental tensor of the Riemann space V n .
[ Length of vector, scalar product and angle of two vectors, adjoint tensor ] The definitions of scalar ( field ) , vector ( field ) , tensor ( field ) , etc. in Riemann space are similar to the previous sections, and their operations The rules are also similar .
Let it be a contravariant vector, then the square of its length is![]()
g ij a i a j
If and are two contravariant vectors, their scalar product is![]()
![]()
g ij a i b j
The cosine of the angle between the two vectors is

Assume
g ij a i = a j , g ij b i = b j
Then and are covariant vectors, their length and scalar product are respectively![]()
![]()
g ij a i a j = a j a j
, g ij a i b j
= a j b j
The adjoint tensor of the tensor is![]()
![]() ,
,![]()
where g lj satisfies the equation
![]()
where is the Kronecker notation .![]()
[ Riemann contact and Christopher symbol ] In Riemann space, the contact can always be determined in a unique way , satisfying the conditions:![]()
(i) Affine connections are torsion-free, i.e.![]()
(ii) The parallel movement generated by the affine connection keeps the length of the vector constant .
This is called the Riemann connection or the Levy-Civita connection .![]()
According to the above two conditions, it can be obtained that

![]()
If you remember
![]()
then there are

Sometimes the following notation is used:
![]() and
and![]()
They are called Christopher's three-index symbols of the first and second types, respectively .
In addition, there is the equation
![]()
or
![]()
It should also be pointed out that all the results in § 4 concerning the covariant differential method hold for the Riemann connection .![]()
2.
The parallelism of Levi-Civita
The parallel movement in the affine connection space is determined by the affine connection . In the Riemann space V n with the metric tensor g ij , the Riemann connection is used to define the corresponding parallel movement called the Levy- Civita parallel movement .![]()
![]()
Suppose a vector field a i = a i ( t ) is given along a certain curve x i = x i ( t ) in V n , if an infinitesimal displacement is made along this curve, the vector a i ( t ) follows the law ![]()
![]()
change, then the vector a i ( t ) is said to perform a Levi-Civita parallel translation along the curve .
The Levi-Civita parallel motion has the properties:
1 The covariant derivative of the metric tensor g ij is equal to zero, i.e.![]()
![]()
Also ,
![]()
![]()
2 ![]() If the two families of vectors a i ( t ) and b i ( t ) move parallel to the curve, then
If the two families of vectors a i ( t ) and b i ( t ) move parallel to the curve, then
![]()
Therefore, the scalar product of the two vectors and the included angle remain unchanged under parallel translation .
3 ![]() The self-parallel curves ( also called geodesics ) in the Riemann space V n are exactly the same as the self-parallel curves in the affine connection space, both of which are determined by the differential equation
The self-parallel curves ( also called geodesics ) in the Riemann space V n are exactly the same as the self-parallel curves in the affine connection space, both of which are determined by the differential equation
![]()
But here is the Riemann connection . So a necessary and sufficient condition for a curve to be a geodesic is that its unit tangent vectors are parallel to each other .![]()
![]()
3.
Curvature in Riemann space
[ Curvature tensor and Lich's formula ] The obvious difference between the covariant derivative of a tensor and the ordinary derivative is that when a higher-order derivative is obtained, the result of the tensor derivative is generally related to the order of the derivative . For example, when an operation acts on a vector , then there are![]()
![]()
 (1)
(1)
remember

It is a third-order covariant and first-order contravariant fourth-order mixed tensor, called the curvature tensor or Riemann-Christopher tensor of space V n .
![]()
The left side is called the staggered second-order covariant derivative of the contravariant vector ; the staggered second-order covariant derivative with respect to the covariant vector is![]()
![]()
![]()
The interleaved second-order covariant derivative of a tensor is
![]()
This is called the Leach formula .
[ Riemann notation · Lich tensor · Curvature scalar · Einstein space ]
covariate component of curvature tensor
![]()
are called Riemann symbols of the first kind, and Riemann symbols of the second kind .![]()
The curvature tensor shrinks to get
![]()
is called the Ricci tensor . The Ricci tensor is then contracted to get
R = g kl
R kl
called the curvature scalar .
If the Leach tensor satisfies
![]()
This space is called Einstein space .
[ Properties of Curvature Tensors ]
1 The first two indices j and k of the curvature tensor are antisymmetric, i.e.![]()
![]()
very
![]()
2 ![]() The curvature tensor performs cyclic permutation of the three covariant indicators and adds them, so that
The curvature tensor performs cyclic permutation of the three covariant indicators and adds them, so that
![]()
This is called the Lich identity .
3 ![]() The first kind of Riemann symbol R kjlr can be calculated as follows:
The first kind of Riemann symbol R kjlr can be calculated as follows:
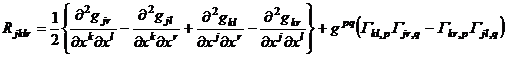
Therefore , R kjlr is antisymmetric with respect to indexes j , k and l , r; it is symmetric with respect to the former pair of indexes and the latter pair of indexes; after cyclic permutation of the first three indexes, the sum is equal to zero, that is,
R jklr = - R kjlr
R jklr = -R jkrl _
R jklr = R lrjk
R jklr + R kljr + R ljkr = 0
4 The Lich tensor is symmetric, that is, R kl = R lk .![]()
At any point in the 5 ![]() space V n , the following formula holds:
space V n , the following formula holds:
![]()
This is called the Pianchi identity . It states that the sum obtained by cyclic permutation of the index ( i ) of the covariant derivative and the first two indices ( j , k ) of the curvature tensor is equal to zero .
[ Riemann curvature ( section curvature ) and constant curvature space ] do the sum of two linearly independent vectors at a point M in the Riemann space V n![]()
![]()
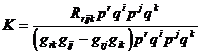
This is called the Riemannian curvature of the plane determined by p i , q i , also known as the section curvature .
If for all points in space V n ( n > 2) we have
R rijk = K ( g rk g ij − g rj g ik )
Then the Riemann curvature K is a constant, which is Schur 's theorem .
A space V n with a constant Riemann curvature is called a space of constant curvature, and the line elements of this space can be transformed into the form

This is called a measure of a space of constant curvature in Riemann form .
A space with constant curvature is an Einstein space .