§ 4 Number Theoretical Functions
A function f ( n ) that has a definite value for any positive integer n is called a number-theoretic function .
[ Integral function and complete integral function ] If ( m, n ) = 1, there is f ( mn ) = f ( m ) f ( n ), then the number -theoretic function f ( n ) is called an integral function . If for any Positive integers m and n both have f ( mn ) = f ( m ) f ( n ), then f ( n ) is called a completely integral function .
The integral function has the following properties :
1 ° If f ( n ) is a non-zero integral function , then f (1)=1 .
2 ° If both g ( n ) and h ( n ) are integral functions , then g ( n ) h ( n ) are still integral functions . And

is also an integral function , where å is the sum over all the different factors d of n .
3 ° If g ( n ) is a non-zero integral function , and , then ![]()

is also an integral function .
4 ° If f ( n ) is an integral function , then
f ([ m,n ]) f (( m,n ))= f ( m ) f ( n )
where ( m, n ) is the greatest common factor of m and n , and [ m, n ] is the least common multiple of m and n .
[ Mobius function ] function

called the Mobius function .
The Mobius function has the following properties :
1 ° 
2 ° μ ( n ) is an integral function , but not a completely integral function .
3 ° Let , if f ( n ) is an integral function , then ![]()
![]()
![]()
is also an integral function . For example
![]()
![]()
![]()
![]()
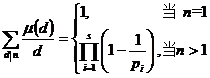

[ Eulerian function ] Let n be a natural number , and ( n ) be ![]() the number of positive integers not exceeding n and co -prime to n , called Euler function .
the number of positive integers not exceeding n and co -prime to n , called Euler function .
The Euler function has the following properties :
1 ° ( n ) is an integral function , but not a fully integral function . ![]()
2 ° If , then ![]()

In particular , when p is a prime number ,
![]()
3 ° ![]()
4 ° 
[ Divisor function ] The number of all factors of the natural number n is called the divisor function , denoted as d ( n ). The divisor function has the following properties :
1 ° d ( n ) is an integral function , but it is not a completely integral function . For any natural numbers m, n , there is often
![]()
2 ° If , then ![]()

[ Von Mangoth function ] function
L ( n )
is called the von Mangoth function . L ( n ) nonintegral function .
[ Mobius inversion formula and Mobius transformation ]
Once the 1 ° inversion formula is set , let h ( k ) be a non-zero complete integral function . If for all suitable h there is always ![]()
![]()

Then for the above h also often have
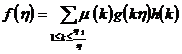
The opposite is true .
Let H ( k ) be a non - zero completely integral function . If for all suitable x we have ![]()
![]()
![]()
Then for the above x also often have
![]()
The opposite is true .
3 ° Inversion formula 3 is set as , and h ( k ) is set as a non-zero completely integral function . If for all constant ![]()
![]()


Then for the above n also often have

The opposite is true .
4 ° Mobius transform Let n be a positive integer , if
![]()

but

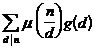
g ( n ) is called the Mobius transform of f ( n ) , and f ( n ) is called the inverse Mobius transform of g ( n ) .
5 ° product Mobius transform Let n be a positive integer , if
![]()
but
![]()
g ( n ) is called the product Mobius transform of f ( n ) , and f ( n ) is called the inverse product Mobius transform of g ( n ) .
[ Mobius transformation table ]
![]()

|
g ( n ) |
f ( n ) |
|
|
|
|
|
|
|
1 |
|
|
d ( n ) |
1 |
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
L ( n ) |
- log n |
|
log n |
L ( n ) |

