§ 3 Random processes
1. General random process
[ Definition of Random Process ] For each t Î T ( T is a fixed set of real numbers ), x ( t ) is a random variable, and the family of such random variables { x ( t ) , t Î T } is called stochastic process. The result of an experiment of a stochastic process is a function defined on T , which is called a realization of a stochastic process. When the variation range T of the parameter t is a set of integers, then it is called
x ( t ), t =0, ± 1, ± 2, L
is a random sequence.
When T contains only one or a finite number of elements, { x ( t ) , t Î T } is the random variable or random vector studied in probability theory.
[ Finite-dimensional distribution function family of random processes ]
Let { x ( t ) , t Î T } be a random process, for any positive integer n and any t 1 , t 2 ,
L , t n Î T , random variables The joint distribution function of x ( t 1 ) , x ( t 2 ) , L , and x ( t n ) is
![]()
A family of finite-dimensional distribution functions called It not only characterizes the statistical regularity of the random variable x ( t ) corresponding to each t , but also characterizes the relationship between each random variable x ( t ) , thus completely describing the statistical regularity of the random process .![]()
[ Statistical parameters of random process ] Let { x ( t ) , t Î T } be a complex-valued random process ( meaning that its real and imaginary parts are real random processes ) . The main statistical parameters are:
1 ° Mathematical expectation (mean) of the mean function for each t Î T , random variable x ( t )
![]()
is called the mean function of a random process, where F t ( x ) is the distribution function of x ( t ) .
2 ° covariance function and variance function for any s , t Î T ,
![]()
is called the covariance function ( or correlation function ) of a random process , where m ( t ) is the mean function.
In particular, when s = t , then it is called
![]()
is the variance function ( or autocorrelation function ) of a random process .
3 ° Higher-order moments for any positive integer n
, non-negative integers m 1 , m 2 , L , m n , m= m 1 + m 2 + L + m n and any real numbers t 1 , t 2 , L , t n , the mathematical expectation of the random variable exists, then![]()

Call it an m -order moment of x ( t ) at t 1 , t 2 , L , t n moments .
[ Mean-square continuity of random processes ] Let { x ( t ) , t Î T } be a random process, t 0 Î T , if
![]()
which is
![]()
Then x ( t ) is said to be mean square continuous at t = t 0 , where lim means mean square convergence. If x ( t ) is mean square continuous for any t Î T , then x ( t ) is mean square continuous on T.
The following three propositions of random process { x ( t ) , t Î T } are equivalent:
1 ° random process { x ( t ) , t Î T } is mean square continuous on T ;
2 ° The covariance function R ( s , t )( s , t Î T ) of a random process { x ( t ) , t Î T } is continuous with respect to s , t ;
The covariance function R ( s , t )( s , t Î T ) of a 3 ° random process { x ( t ) , t Î T } is continuous with respect to s , t on the diagonal s = t .
Special types of random variables are described below:
[ Independent random process ]
If for any positive integer n and any arbitrary t 1 , t 2 , L t n Î T , the random variables x ( t 1 ), x ( t 2 ), L , x ( t n ) are independent of each other, that is

Then { x ( t ) , t Î T } is said to be an independent random process.
[ Normal process ] If for any positive integer n and any t 1 , t 2 , L , t n Î T , the random variables x ( t 1 ), x ( t 2 ) , L , x ( t n ) The joint distribution is always normal, i.e.
![]()

Then { x ( t ) , t Î T } is a normal (or Gaussian) process, where R jk = R ( j , k ), ( R jk ) is called a covariance matrix ; ( R jk ) is ( R jk ) jk ) inverse matrix.
[ Markov Process ]
If for any n = 1,2, L and any t 0 , t 1 , L , t n Î T ( where t 0 < t 1 < L < t n ) and any real number x , y , the equation
P { x ( t n ) ≤ y | x ( t n -1 )= x , x ( t n- 2 )= x n- 2 , L , x ( t 0 )= x 0 }= P { x ( t n ) ≤ y | x ( t n- 1 )= x }
For all x ( t n- 1 ), L , x ( t 0 ) , it is called { x ( t ) , t Î T } is a Markov process, abbreviated as Markov process.
[ Time-aligned Markov Process ] Let { x ( t ) , t Î T } be a Markov process, if for any t 1 Î T , t 2 Î T
( t 1 < t 2 ) , conditional distribution
![]()
That is, the conditional distribution F ( t 1 , x ; t 2 , y ) only depends on t 2 - t 1 , x , y , then { x ( t ) , t Î T } is a time- aligned ) of the Markov process.
[ Random process with independent increments ] If for and any group , where ), the random variables , , ¼ , are independent of each other, then it is called a random process with independent increments.![]()
![]()
![]()
![]()
![]()
![]()
![]()
[ Random Process with Stationary Increment ] If for any t 1 , t 2 Î T and any h ( t 1 + h , t 2 + h Î T ) , the random variable
x ( t 2 + h )( t 1 + h ) and ![]() x ( t 2 )( t 1 )
x ( t 2 )( t 1 )![]()
Following the same probability distribution, it is called a random process with stationary increments.![]()
[ Poisson process ] Let { x ( t ) , 0 ≤ t < ∞ } be a random process with stationary independent increments taking non-negative integer values. If for any t ( 0 ≤ t < ∞ ) , the relation
![]() ( k =0 ,1,2 , L )
( k =0 ,1,2 , L )
is established ( where λ > 0 is a constant ) , then { x ( t ) , 0 ≤ t < ∞ } is called a Poisson process.
[ Wiener process ]
If the random process { x ( t ) , 0 ≤ t < ∞ } satisfies P ( x (0)=0)=1 , has a stationary independent increment, and the distribution density function of the random variable x ( t ) Yes
![]()
Then { x ( t ) , 0 ≤ t < ∞ } is called a Wiener process or a Brownian motion process.
[ Stationary Process ]
If for n =1,2, L , any t m Î T ( m =1,2, L , n ) and any τ ( t m + τ Î T , m =1,2, L , n ) , the equation
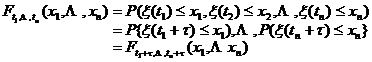
is established, then { x ( t ) , t Î T } is a stationary process ( a stationary process in the narrow sense ) .
The Markov process
1. Transition probability
[ State and State Transition Probability ] Consider a series of random trials , in which the results of each trial can be listed as one of two mutually exclusive events E 1 , E 2 , L and only one of them occurs, then these events E i are called ( i = 1, 2, L ) is the state. If E i occurs, the system is said to be in state E i . Use p ij ( t , τ ) to denote the conditional probability that " under the condition that the system is in state E i at time t , the system is in state E j at time τ ( t > τ ) ", called pij ( t , τ )is the transition probability.
[ No After Effects and Time Homogeneity of the Process] Without After Effects If the state of the system at time t 0 is known, the situation where the system will reach the state after time t 0 is the same as the state the system was in before time t 0 If the state is irrelevant, the process is said to be ineffectual.
Time-homogeneous If the transition probability p ij ( t , τ ) is only related to i , j , τ , the process is called time-homogeneous, abbreviated ![]()
p ij ( τ ) = p ij ( t , t + τ )
2. Markov chain
[ Markov chain ] A Markov chain is a Markov process in which time and state are discrete .
1 ° Under a series of random experiments, the possible discrete states of the system are E 0 , E 1 , L , if for any two positive integers k , m , any integer 0 ≤ j 1 < j 2 < L < j l < m , the equation
![]()
All are established ( ![]() representing the event of " the occurrence of Em in the mth trial " ) , then this random trial is called a Markov chain, or Markov chain for short.
representing the event of " the occurrence of Em in the mth trial " ) , then this random trial is called a Markov chain, or Markov chain for short.
2 ° Sequence of random variables { x n } ( n = 0,1, L ) is the definition of Markov chain
Let { x n }( n= 0,1, L ) be a sequence of random variables, each of which may take a value ( equivalent to the state E i ) x i ( i =0,1,2, L ) , if for any positive integer k , m , any positive integer 0 ≤ j 1 < j 2 < L < j l < m , the equation
![]()
If established, { x n } is called a Markov chain, or Markov chain for short.
It is usually desirable to take { x i }={1,2, L } .
The random test sequence delineated by the Markov chain can be intuitively understood as to test the state of the "future" as long as the known state of the "present" is used, and the state of the "past" has no effect. Aftereffects.
Markov chains, so that Markov processes are random processes with no aftereffects.
[ Transition probability matrix of Markov chain ] If the probability of the system going from state E i to state E j through a transition at time m is independent of time m , then p ij can be used to represent this transition probability. obviously
![]() ( p ij ≥ 0, i , j =0,1,2, L )
( p ij ≥ 0, i , j =0,1,2, L )
The transition probability p ij can be arranged into a transition probability matrix

This is a matrix of non-negative elements whose elements in each row sum to 1 , called the one-step transition probability matrix of the Markov chain.
It is also used to represent the transition probability of the system from state E i to reach E j after n transitions,![]()
Also define the n- step transition probability matrix of the Markov chain :
![]()
From no aftereffect, we get
![]()
It is called the Chepman - Kolmogorov equation.
From the Chepman - Kolmogorov equation it can be derived
P ( n ) = Pn _
[ Classification of Closed Sets and States ] Consider a time-homogeneous Markov chain . Let E be the state space, E = ( E 0 , E 1 , E 2 , L ), if there is a positive integer n such that E k is said to be reachable from E j , and denoted as E j T E k . . If E j T E k and E k T E j , say E j , E k , communicate with each other, denoted as E![]() j Û E k .
j Û E k .
A subset C of E is called a closed set, which means that no state outside C can be reached from any state in C. Let E be a closed set, if the single-point set { E k } is a closed set, then E k is called an attractive state. If there is no proper subset in E , it is a closed set, and the Markov chain is said to be inseparable.
Denote the conditional probability of "the system is in state E i and firstly transitions to state E j after n steps " , it can be expressed as the transition probability as![]()

then
![]()
remember
![]()
It is the conditional probability that " the system finally reaches state E j after finite transitions under the condition that it is in state E i at the beginning", and let
![]()
If f ij =1, then m ij can be regarded as the mathematical expectation of the number of transitions from state E i to state E j for the first time
The statuses are categorized as follows:
1 ° If f jj =1 , then E j is said to be constant ; if f jj <1 , then E j is said to be very recurrent;
2 ° Let E j be a constant return state, if m jj = ∞ , then E j is called negative constant return ( or zero state ) ; if μ jj < ∞ , then E j is called positive constant return ( or positive state) ) .
3 ° If the positive integer has the greatest common divisor t , when t >1 , E j is called periodic , or has period t ; when t = 1, E j is called non-periodic. ![]()
4 ° E j is said to be ergodic if E j is a constant, aperiodic positive state .
Discriminant method for state classification
1 ° E j is a necessary and sufficient condition for very return
.![]()
2 ° If E j is a constant return state with period t
, then .![]()
3 ° If E j is ergodic
, then .![]()
4 ° If E j is constant
, then it is a sufficient and necessary condition for the zero state .![]()
[ Decomposition theorem of Markov chains ] The state space of any system can be decomposed into the sum of the following disjoint subsets D , C 1 , C 2 , L , where
1 ° Any C j is an inseparable closed set composed of always-returning states , and the states in C i cannot be reached from the states in C j ( i ≠ j ) ;
2 ° The states in C j are homogeneous : either all zero, or all ergodic, or all nonzero states with periods ( in either case, the states in C j have the same period ) , and f ik =1( E i Î C j , E k Î C j ) ;
3 ° D consists of all non-recurrent states ( states in C j may arrive from states in D , but not vice versa ) .
[ The ergodicity theorem of Markov chains ] For different types , there are the following ergodicity theorems:
1 ° If E k Î D or E k is zero, then for any j , we have
![]()
2 ° If E k is a normal return state with period t , then for any j , we have
![]() (1 ≤ r ≤ t )
(1 ≤ r ≤ t )
in
![]()
Represents the probability of arriving at E k for the first time at a certain n steps ( n ≡ r (mod t )) starting from E j .
3 ° For inseparable aperiodic Markov chains , the limit
![]()
exists, and only in the following two cases:
( i ) All p j ( probability of appearing E j ) are greater than zero, at this time { p j } is the only stationary distribution, that is, the probability distribution { p j } satisfies
![]() ( j =0,1, L )
( j =0,1, L )
( ii ) All pj are equal to zero, in which case there is no stationary distribution.
3. Markov process with continuous time and discrete state
Only the Markov process of Shiqi is considered here .
[ Cherman - Kolmogorov equation ] Let p ij ( t ) denote the probability of the system transitioning from state E i to state E j at time interval t , then
![]() , p ij ( t ) ≥ 0
, p ij ( t ) ≥ 0
For t > 0, τ > 0 there is the Cherman - Kolmogorov equation
![]()
It is the basis of Markov process research.
[ Ergodicity theorem ] Any time - continuous Markov process with finite state ( E 1 , L , En ) , if there is a t 0 such that for any i , r , p ir ( t 0 )>0, then limit
![]() ( 0 ≤ j , i ≤ n )
( 0 ≤ j , i ≤ n )
exists and is independent of i .
[ Kolmogorov's forward and backward equations ]
If a Markov process with only a finite number of states satisfies
![]()
It is called a stochastic continuous Markov process.
For stochastic continuous Markov processes with finite states, there are Kolmogorov's forward and backward equations:
![]() ( forward equation )
( forward equation )
![]() ( backward equation )
( backward equation )
in
![]()
4. Diffusion process
[ Definition of Diffusion Process ] A state-continuous Markov process { x ( t ) , 0 ≤ t < ∞ } , if its condition
The distribution function F ( t , x ; τ , y ) for any ε > 0 and t 1 < t < t 2 , t 1 → t , t 2 → t , holds the following three relations about x consistently:
( i )![]()
( ii )![]()
( iii )![]()
The Markov process { x ( t ) , 0 ≤ t < ∞ } is called a diffusion process.
[ Kolmogorov's first equation ]
If the partial derivative of the conditional distribution function F ( t,x ; τ , y ) of the diffusion process
![]()
exists and is continuous for any t , x ,
y and τ ( τ > t ) , then the function F ( t , x ; τ , y ) satisfies Kolmogorov's first equation
![]()
[ Kolmogorov's Second Equation ] If the conditional distribution function F ( t , x ; τ , y ) of the diffusion process has a distribution density f ( t , x ; τ , y ) , and the following partial derivatives
![]()
exists and is continuous, then f ( t , x ; τ , y ) satisfies Kolmogorov’s second equation
![]()
3. Stationary Stochastic Process
[ Weakly stationary process ] If the random process { x ( t ), t Î T } satisfies

It is called a weakly stationary process ( or a generalized stationary process ) .
A stationary process in the broad sense is not necessarily a stationary process in the narrow sense; conversely, a stationary process in the narrow sense is not necessarily a stationary process in the broad sense, but if the second moment of the stationary process in the narrow sense exists, then it must be a stationary process in the broad sense.
For a normal process, generalized stationarity and narrowly defined stationarity are the same.
In theoretical studies, it is often more convenient to consider complex-valued stochastic processes. The so-called complex-valued random variable x refers to x = η + i x , where η and x are both random variables; and the complex-valued random process is x ( t ) = η ( t ) +
i x ( t ) , where η ( t ), x ( t ) are real-valued random processes.
The mean ( or mathematical expectation ) of a complex-valued random variable x = η + i x is defined as
![]()
The correlation moments of two complex-valued random variables x 1 , x 2 are defined as
![]()
The generalized stationarity of a complex-valued random process { x ( t ), t Î T } is that it satisfies

All complex-valued generalized stationary processes are considered below.
[ Spectral decomposition of correlation function ]
If the function R ( τ ) is the correlation function of a mean square continuous stationary process { x ( t ), < t < } ![]()
![]() , then
, then
![]()
Where F ( λ ) is a bounded non-decreasing function, satisfying , is called the spectral function of the stationary process { x ( t ), < t < } ( called spectrum in engineering ) .![]()
![]()
![]()
If F ( λ ) is absolutely continuous, denoted as spectral density ( called spectral density in engineering ) , then![]()
![]()
![]()
When { x ( t ), < t < } ![]()
![]() is a real-valued stationary process, the correlation function R ( τ ) can be expressed as
is a real-valued stationary process, the correlation function R ( τ ) can be expressed as
![]()
or ( when spectral density exists )
![]()
Where F 1 ( λ )=2 F ( λ )+ c ( c is a constant ) , .![]()
In particular, for complex-valued stationary sequences { x n , n =0, ± 1, L } we have
![]() ( k =0 , ± 1, L )
( k =0 , ± 1, L )
where the spectral function F ( λ ) satisfies
F ( )=0, F (![]() p )= R (0)
p )= R (0)
[ ergodicity theorem ]
1 ° If { x ( t ),- ∞ < t < ∞ } is a mean square continuous stationary process, then
![]()
The necessary and sufficient conditions are:
![]()
2 ° If
{ x n , n =0, ± 1, L } is a stationary sequence, then
![]()
The necessary and sufficient conditions are:
![]()
3 ° If { x ( t ),- ∞ < t < ∞ } is a mean-square continuous stationary process with zero mean, and for the constant t > 0, it is also a mean-square continuous stationary process, record its correlation function is R t ( u ) , then
![]()
![]()
![]()
The necessary and sufficient conditions are:
![]()
4 ° If
{ n = 0, ![]() ± 1, L } is a stationary sequence with zero mean, and a fixed integer m , n = 0, ± 1, L } is also a stationary sequence, denote its correlation function as R m ( k ) , then
± 1, L } is a stationary sequence with zero mean, and a fixed integer m , n = 0, ± 1, L } is also a stationary sequence, denote its correlation function as R m ( k ) , then ![]()
![]()
The necessary and sufficient conditions are:
![]()
The ergodicity theorem shows that for a stationary process, as long as it satisfies the conditions of the theorem ( in practice they are often satisfied ) , then the average of the sample space ( such as mean, correlation moment, etc. ) can be replaced by the average of time, More specifically, the mean and correlation function of the process can be determined as long as the stationary process is realized once over a sufficiently long time. This is exactly why the ergodicity theorem is practically important.
[ spectral expansion of stationary process ]
If { x ( t ),- ∞ < t < ∞ } is a mean-square continuous stationary process with zero mean, then we have
![]()
in
![]()
Satisfy ( i ) EZ ( l )=0
( ii ) when the interval and do not overlap![]()
![]()
![]()
( i.e. Z ( l ) is a process with orthogonal increments )
( iii ) ( F ( l ) is the spectral function )![]()
Z ( l ) iscalledthe random spectral function of x ( t ), and the integral expression of x ( t ) is called the spectral expansion of x ( t ).
In particular, if x ( t ) is a real-valued mean-square continuous stationary process, then we have
![]()
in
![]()
![]()
Satisfy ( i ) EZ 1 ( l )= EZ 2 ( l )=0,
( ii ) when the interval and do not overlap![]()
![]()
![]() ( j , k =1,2)
( j , k =1,2)
( iii )![]()
( F ( l ) is the spectral function )
If { x n , n =0, ± 1, L } is a stationary sequence with zero mean, then
![]()
where the random spectral function Z ( l ) is
![]() ( - p ≤ λ ≤ p )
( - p ≤ λ ≤ p )
It also satisfies the properties ( i ) ~ (iii) similar to the random spectral functions of the mean square continuous stationary process .