§ 2 Conformal Mapping
1. Conformal mapping and its properties
[ Conformal mapping and its necessary and sufficient conditions ] If the mapping of the function in the neighborhood of any point in the region satisfies the conditions: ( i ) the scalability is unchanged (§ 1 , a), ( ii ) the rotation angle is unchanged, and keeps Orientation of angles (§ 1 , a), then the mapping of the function is said to be a conformal mapping (conformal transformation) in the region .![]()
![]()
![]()
![]()
![]()
![]() A necessary and sufficient condition for a conformal mapping within a region is that it is analytic within is not equal to zero everywhere within .
A necessary and sufficient condition for a conformal mapping within a region is that it is analytic within is not equal to zero everywhere within .![]()
![]()
![]()
![]()
![]()
[ Properties of Conformal Mapping in Region D ]![]()
The image of any infinitesimal circle within 1 o D is a circle within a degree of difference of a higher order infinitesimal .
The included angle of two curves within 2 o D remains unchanged after mapping (conformal) .
3 o The image of any region in D (including D itself) is a region .
4 o At any point in D , neither the maximum nor the minimum can be reached . ![]()
Every point z in 5o D has a neighborhood, and in this neighborhood, it is unilobal . ![]()
2. Fractional linear mapping and its properties
Fractional Linear Function
![]()
The implemented mapping is called a fractional linear mapping (fractional linear transformation) . Its inverse mapping
![]()
It is also a fractional linear mapping . The specified and corresponding to and respectively , when c = 0 , the specified corresponding , then the fractional linear mapping determines a one-to-one correspondence between an extended plane and an extended plane . At the same time, except for the point is outside the first-order pole, and resolves everywhere on the extended plane .![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Conversely, a function must be a fractional linear function if it has a single leaf on the extended plane and resolves everywhere except one point, which is the first-order pole of the function .![]()
![]()
![]()
![]()
Fractional linear maps have properties:
1 o is conformal everywhere on the extended plane (the angle between the two straight lines is defined as the angle between the two curves after the transformation of the two straight lines ) . ![]()
![]()
![]()
2 o Under the fractional linear transformation, the circle still becomes a circle (a straight line is regarded as a circle with infinite radius) .
3 o With respect to a point of symmetry of a circle or a line (see § 2 , footnote to 3) the image after mapping maintains symmetry .
4 o There is a unique fractional linear mapping that maps any three points plane to any three points on the plane , such a fractional linear mapping is ![]()
![]()
![]()
![]()
![]()
5 o For any circle on the extended plane, a fractional linear mapping can be found to map it to any circle on the extended plane . ![]()
![]()
6 o Under the fractional linear map, the intersection ratio of the four points remains unchanged ( the intersection ratio of is ) . Note that a sufficient and necessary condition for the four points to be co-circular (or collinear) is that their intersection ratio is a real number .
![]()
![]()
![]()
3. Simple Fractional Linear Mapping
|
graphics |
illustrate |
|
[ pan map ] |
map translate the figure by a complex number |
|
[ Scaling and Rotation Mapping ]
|
map Extend and retract the mold around the origin, and then rotate it by an angle around the origin |
|
[ inversion map ]
|
map Map a point inside (outside) the unit circle to a point outside (inside) the circle (the two points are on a ray passing through the origin, and their moduli are reciprocals of each other), and then map this image point to its real axis on a symmetrical point .
point sum is a fixed point |
|
[ Mapping of upper half plane to upper half plane (or lower half plane) ]
|
map ( i ) When all are real numbers, the real axis of the plane is mapped to the real axis of the plane ( ii ) At that time , map the upper half plane to the upper half plane ( Figure ( )) . ( iii ) At that time , map the upper half- plane to the lower half- plane (Fig. ( b )) . |
|
graphics |
illustrate |
|
[ Mapping of the upper half plane to the inside of the unit circle ] ( mapped to ) |
map ( is a real number, ) maps a given point in the upper half-plane to the center of the unit circle, and the point maps to .
Corresponding to the bundle of radii within the unit circle are the arcs (that fall in the upper half-plane ) of the family of circles passing through the sum of the points; to the family of concentric circles centered on the circle are those that make the sum a pair of symmetrical points * family circle |
|
[ Mapping from inside the unit circle to inside the unit circle ] (a point inside the circle is mapped to )
|
map ( is a real number, ) Map a point in the known circle to the center of the circle , map the symmetrical point of the point about the unit circumference to the symmetrical point about the unit circle , and the corresponding curves are marked in the figure |
Fourth, the principle of symmetry and polygon mapping
[ Principle of Symmetry ] Let sum be two regions on the plane that are symmetrical about their common boundary (a segment of an arc), and sum be two regions on the plane that are symmetrical about their common boundary (a segment of an arc) .![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
If a function satisfies the following conditions: ( i ) maps conformal to ; ( ii ) is continuous on , maps unilobe to . Then there exists a function with the property:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
1 o Map the area conformally to the area . ![]()
![]()
![]()
2o included , . ![]()
![]()
3 o Map two points about symmetry in the region to two points about symmetry in the region . ![]()
![]()
![]()
![]()
[ Polygon mapping ] Polygon mapping is a mapping that maps a half-plane to a polygon .
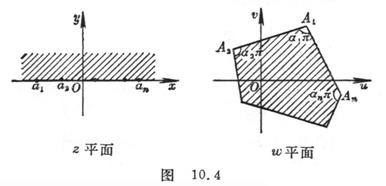
Suppose there is a point on the real axis of the plane, a side of the plane, the vertex is , the vertex angle at the point is , then the Schwartz - Christopher integral![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
|
![]() are three constants) map the upper half-plane of the plane to the interior of the given polygon , and the points on the real axis of the plane are respectively mapped to the vertices of the polygon of the plane (Figure 10.4 ) .
are three constants) map the upper half-plane of the plane to the interior of the given polygon , and the points on the real axis of the plane are respectively mapped to the vertices of the polygon of the plane (Figure 10.4 ) .![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
If the point at infinity (let ) of the plane corresponds to a vertex (let) of the polygon , then the mapping simplifies to![]()
![]()
![]()
![]()
![]()
Example Rectangle mapping maps the upper half of a plane to the interior of a rectangle on the plane (Figure 10.5 ) . ![]()
![]()
![]()
![]()
|
|
Solution First, consider the mapping of the first quadrant of the plane to the right half of the interior of the rectangle . At the same time , let the preimage be denoted by , the desired mapping is![]()
![]()
![]()
![]()
![]()
![]()

Because of , so , because of . so![]()
![]()
![]()
 ( 1 )
( 1 )

i.e. ( 2 )
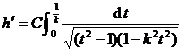
Assuming that the constants are known, the length and width (that is, the sum ) of the rectangle are appropriately selected , so that the constants in ( 1 ) and ( 2 ) are used . ![]()
![]()
![]()
![]()
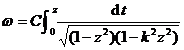
This is an elliptic integral of the first kind (Chapter XII, § 1 , x) .
5. The existence and uniqueness theorem of conformal mapping (Riemann's theorem)
With two exceptions (extended plane or extended plane minus a point), there is the following existence and uniqueness theorem for conformal mappings for simply connected regions:
Assuming that there is more than one boundary point of the simply connected region (not included ) on the plane , then there is a unique single-leaf analytic function on the plane that maps the single-leaf conformal angle to the interior of the unit circle , while satisfying![]()
![]()
![]()
![]()
![]()
![]()
![]()
( i )![]()
( ii ) is a constant .![]()
![]()