Chapter 10 Complex Variable Functions
The object of this chapter is the complex-valued function defined on the complex number field (complex variable function for short) . The focus is on a special kind of complex variable function — analytical function . The main content includes the analytical properties of the analytical function (calculus theory and level number representation), geometric properties (conformal mapping), etc.
§ 1 Analytical functions
1. Basic Concepts of Complex Functions and Derivatives of Complex Functions
[ Single-valued and multi-valued functions ] Let Σ be a region on the extended complex plane (that is, the plane containing the point ∞ at infinity) z (Chapter 21 § 5 , II), for each complex number z in Σ , according to a certain rule, there is one or more complex numbers ω corresponding to it, it is said that a complex variable function is defined on Σ , denoted as
![]()
The region Σ is called the domain of the function .![]()
If each complex number z has only one complex number ω corresponding to it (allowing different complex numbers z to correspond to the same complex number ω ), the function is said to be single-valued; if some complex number z has multiple ω values corresponding to it, then A function is said to be multi-valued . If no description is given below, it will always refer to a single-valued function .
[ Mapping · Image · Preimage ] If the complex number z is represented by a point on the complex plane z (referred to as the z plane), and the complex number ω is represented by a point on the complex plane ω (referred to as the ω plane), then the complex variable function is the area on the z plane. The correspondence between the points of Σ and a set of points on the ω plane (Chapter 21 § 3 , a) the points of F. In this way, the complex variable function can be regarded as a geometric "map" (transformation ) ( Chapter 21 § 1 , 2), the point ω ( ) is called the image of the point z (image point), and the point z is called the original image (image source) of the point ω . Generally, when the point z is in the complex When a figure A (or point set) is drawn on the plane z , correspondingly, its image point![]()
![]()
![]() ω draws a figure (or point set) on the complex plane ω . B. Call B the image of A , and A is the original image of B. Call the function to map A onto B.
ω draws a figure (or point set) on the complex plane ω . B. Call B the image of A , and A is the original image of B. Call the function to map A onto B.![]()
[ Single-leaf function and multi-leaf function · inverse function ] If the function is single-valued on the point set A, and for any two different points z 1 and z 2 on the point set A , their image ω 1 = f ( z 1 ) and ω 2 = f ( z 2 ) are also different, then the function is said to be unilobal on the point set A , if there are at least two different points z 1 and z 2 on the point set A , then the function is called is leafy on point set A.![]()
![]()
![]()
![]()
If the single-valued function is again unilobal, it represents a one-to-one correspondence between the points of A and B , and for each point ω on B , there is one and only one point z on A that corresponds to it . do![]()
![]()
It is called the inverse of a function (single-valued) .![]()
If the function is not unilobal on the point set A , then its inverse function is multivalued .![]()
[ Mapping theorem of two-sided single-valued continuity ]
Let ω = f ( z ) be a single-valued continuous function in the z - plane region Σ , if it is unilobal again, then the image Δ of Σ is still a region, and the inverse function is in Continuity within Δ . This kind of mapping whose two sides are single-valued is continuous is called topological mapping or homeomorphic mapping .![]()
[ Limit of complex variable function ] Let z 0 be a point in the domain of the function f ( z ) , if for any small positive number ε , there is a positive number such that for any complex number z (complex number z 0 ) that satisfies the condition ∣ itself may be excluded), both![]()
![]()
![]()
Then the complex number A (finite or infinite) is called the limit of the function ω = f ( z ) when z tends to z 0 , denoted by
![]()
[ Continuity and Continuity of Complex Functions ]
Let z 0 be a point in the domain of the function f ( z ) , if the function ω = f ( z ) has a finite limit when z → z 0 , and at the same time satisfy
![]()
Then the function ω = f ( z ) is said to be continuous at point z 0 , and if the function ω = f ( z ) is continuous at every point on the region Σ , the function ω = f ( z ) is said to be continuous on the region Σ .
If for any small positive number ε , there is a positive number δ = δ ( ε ) , so that any two points z 1 and z 2 in the region Σ that satisfy the conditions have![]()
∣![]()
Then the function f ( z ) is said to be uniformly continuous on Σ .
The function is consistent and continuous on the region Σ , it must be continuous on the Σ , and conversely, the function is continuous on the region Σ , which does not necessarily guarantee that the function is consistent on the Σ . However, if Σ is a bounded closed region (denoted as ) , then the above The continuity and consistent continuity are equivalent . At the same time, the continuous function ω = f ( z ) on the bounded closed region has two other properties similar to the continuous function on the closed interval in differential calculus :![]()
![]()
![]()
1 o If the function ω = f ( z ) is continuous over a bounded closed region , then there exists a positive number M such that for all z above , there is![]()
![]()
∣![]()
2 o If the function ω = f ( z ) is continuous on a bounded closed region , then the modulus of the function f ( z ) can reach its maximum and minimum values on , that is, there are two points z 1 and z 2 on , such that for all z above , there are![]()
![]()
![]()
![]()
![]()
∣ ∣![]()
[ Derivative of a complex function ]
Let the function ω = f ( z ) be defined on the region Σ , z 0 being a point within Σ , if the limit
![]()
exists and is finite, then this limit is called the derivative of the function f ( z ) at point z 0 , denoted as
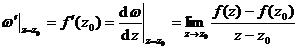
And a function is said to be differentiable at a point (singular, holomorphic) .![]()
![]()
The definition of the differentiability of a complex variable function is the same in form as the definition of the differentiability of a real variable function, so some rules and formulas for the derivative of complex functions and some rules and formulas for the derivatives of real variable functions are also in form. The same . But on the other hand, since in the definition of the differentiability of the complex variable function, the moving point z tends to z 0 on the plane, the way is arbitrary, it can tend to z 0 along any curve , which is It is shown that the conditions for the differentiability of functions of complex variables are more demanding than those for functions of real variables, which brings many unique properties and applications of the theory of complex functions .
[ Geometric meaning of the derivative of a complex function (scaling coefficient and rotation angle) ]
Let the curve C passing through z 0 on the z plane, the image that passes through the mapping ω = f ( z ) (differentiable) is the curve passing through the ω plane , if then![]()
![]()
![]()
1 o ∣ is called the scaling factor of the mapping ω = f ( z ) at z 0 , which is equal to the limit of the ratio of the infinitesimal chord length on the curve passing through ω 0 to the infinitesimal chord length on the curve C passing through z 0 , which is the same as the curve C It has nothing to do with the choice of curve ;![]()
![]()
![]()
2 o is called the rotation angle of the mapping ω = f ( z ) at z 0. If the z plane and the ω plane are superimposed together, so that the point z 0 coincides with the point ω 0 , the x axis is parallel to the u axis and the positive direction is the same , then it is equal to the angle that the tangent of the curve C at z 0 turns to the tangent of the curve at the corresponding point ω 0 , and it has nothing to do with the choice of the curve C and the curve .![]()
![]()
![]()
![]()
2.
Analytical function
In general, the complex function ω = f ( z ) can be written as
![]()
In this way, the discussion of the general complex variable function is equivalent to the discussion of the real variable function of two two variables . However, in production practice and scientific experiments, we often encounter a special kind of complex variable function— —Analytical functions . For this type of function, it is more convenient to study the complex variable function f ( z ) itself than to study the two real variable functions u ( x , y ) and v ( x , y ) separately , and the conclusions are better. Simple and complete, easy to apply .
1. Definition of Analytical Function and Cauchy - Riemann Equation
[ Analytical Functions and the Cauchy - Riemann Equation ] A complex function f (z ) is said to be analytic at point z0 if it is point-point-differentiable within a sufficiently small field * of points z=z0 ; if the function If f ( z ) is point-to-point differentiable in a region Σ , it is said to be analytic (regular, holomorphic) in the region Σ .
If the function defined in the region Σ
![]()
Analyzing in Σ , then u ( x, y ) and v ( x , y ) satisfy the following Cauchy - Riemann equations in Σ
![]()
Conversely, if u ( x, y ) and v ( x , y ) satisfy the above conditions in Σ and are differentiable, then f ( z ) is analytic in Σ . At this time, the derivative of the analytic function f ( z ) It can be expressed in one of the following four forms:

[ Harmonic function ] There is a real variable function u ( x , y ) of second-order continuous partial derivatives in the region Σ , if the Laplace equation is satisfied in Σ
![]()
Then the function u = u ( x , y ) is said to be a harmonic function in Σ .
The real and imaginary parts of the analytic function f ( z ) in the region Σ are harmonic functions .
[ formal derivative ] will be
![]()
or
![]()
Introducing Formal Derivatives as Variable Substitution
![]()
![]()
If f ( x , y ) is a function of real variables x , y with continuous partial derivatives, then
![]()
In this way, the Cauchy - Riemann equation can be written as
![]()
The Laplace equation can be written as
![]()
The Cauchy - Riemann equation in polar coordinates can be written as![]()
![]()
![]()
2. Analysis and development
[ Direct analytic development ] If there are two simply connected regions * with a common boundary Г , and are single-valued analytic within and respectively , continuous on Г and Г , and on Г , then it is called a direct analysis inward through Г Development (or extension) (Figure 10.1 ).![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
[ Analytical development and complete analytic function ] is set as a single-connected region, and has a common boundary , , for any k , single -valued analytic .
And is continuous on and on respectively , and on , then it is called f 1 ( z ) through A series of area- inward analytical development .![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Consider the various analytical developments of f 1 ( z ) through all possible region strings, and consider the values of all these analytical developments as the value of a function F ( z ) . At this time, F ( z ) is called a complete analytic function, and those single-valued analytic functions that compose it, that is , various analytical developments of f 1 ( z ) , are called branches of F ( z ) .
3. Elementary Analytical Functions
[ rational function ]
![]()
In the formula, P ( z ) and Q ( z ) have no common factor, R ( z ) takes the value ∞ at the zero point of Q ( z ) , then R ( z ) is continuous on the extended plane .
When n > m , R ( z ) has a zero of order n - m at ∞ ; when n < m , ∞ is a pole of order m - n of R ( z ) (§ 4 , 1, 3 ); when n = m , have
![]()
On the extended plane, the number of zeros of a rational function (including ∞ is a zero) is equal to the number of poles, which is equal to the larger of m and n , and the order of a rational function is defined by it . Therefore , a rational function R (z) of order k has k zeros and k poles, and each equation R (z) = a ( a is any constant) has k roots (multiple roots count as several roots) .
![]() The rational function when is the commonly used fractional linear function (§ 2 , two and three) .
The rational function when is the commonly used fractional linear function (§ 2 , two and three) .
[ Power function and its inverse ]
1 o power function integer ) is single-valued analysis on the full plane , it maps the extended z plane to the extended ω plane , and ∞ maps to , ∞ respectively , this function is a multi-leaf function on the full plane . ![]()
![]()
![]()
Assume
![]()
but
![]()
The function maps the semi-straight line from the origin to the half-line from the origin , maps the circle from the origin as the center to the circle with the origin as the center, and maps the angular area on the z -plane![]()
![]()
![]()
It is mapped to the crack region with the semi-straight line removed on the ω plane. In the upper angular region , the function is unilobal analytical . Such a region is called the unilobal region of the function , and the z plane can only be divided into n unilobal regions. .![]()
![]()
![]()
2 o functions , integers ) are multivalued functions on the full plane ( ω plane ) because ![]()
![]()
Therefore, for each non- zero sum , there is a point on the plane corresponding to it, and this point is distributed on the vertex of an inscribed regular polygon of the circle .![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The function has n branches![]()
![]()
![]()
Or an n -valued function .![]()
[ Exponential and logarithmic functions ]
1 o exponential function
![]()
is a single-valued analytic function on the full plane, there is no zero point on the full plane, is a periodic function , the period is , ie . When z tends along the real axis ,
, when z tends along the real axis , . So , when there is no The limit can
not be defined on the extended plane .![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
set
, then![]()
![]()
The function maps a straight line to a ray ; maps a line segment to a circle ; maps the strip area to the crack area on the ω plane with the positive real axis removed ; maps the strip area to the upper half plane ; maps all strip areas![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Mapped to the crack region on the ω plane with the positive real axis removed . Therefore , the exponential function is a multi-leaf function on the full plane .
2 o logarithmic function
![]()
The expression is
![]()
Since it is infinitely multivalued , the logarithmic function is an infinitely multivalued function , and corresponds to an integer multiple of the difference between any two function values of the same ω value . Let the main value of the logarithmic function be![]()
![]()
![]()
![]()
then
![]()
band area
![]()
and
![]()
They are all unilobal regions of functions , and there are infinitely many , so functions have infinitely many branches , or infinitely many-valued functions .![]()
![]()
![]()
[ Trigonometric and Inverse Trigonometric Functions ]
1 o The sine function and cosine function are respectively defined by the following equations :
![]()
![]() The sum is a single-valued analytic function on the full plane , and has a period , so it is a multi-leaf function .
The sum is a single-valued analytic function on the full plane , and has a period , so it is a multi-leaf function .![]()
![]()
2o The tangent function and the cotangent function are respectively defined by the following equations :
![]()
![]()
![]() The points removed on the full plane are analytical ; the points removed on the full plane are analytical . They are all periodic functions of the period .
The points removed on the full plane are analytical ; the points removed on the full plane are analytical . They are all periodic functions of the period .![]()
![]()
![]()
![]()
All trigonometric formulas of plane trigonometry are applicable to complex trigonometric functions . It must be noted that in the complex plane and no longer hold, for example , .![]()
![]()
![]()
3 o arc cosine function by solving the equation
![]()
get
![]()
Similarly , there are
![]()
![]()
![]()
Inverse trigonometric functions are infinitely multi-valued functions . Their principal values only need to be replaced by (the principal value of the logarithm) at the right - hand side of the equation .![]()
![]()
[ Hyperbolic and Inverse Hyperbolic Functions ]
1 The definition of a hyperbolic function is :
![]()
![]()
2 o The relationship between hyperbolic functions and trigonometric functions :
![]()
![]()
The definition of the 3o inverse hyperbolic function is :
![]()
![]()
![]()
![]()
Inverse hyperbolic functions are infinitely multi-valued functions, and their principal values only need to be replaced by .![]()
![]()
4. Riemann surface, fulcrum and branch line
[ Riemann surface of n - valued function ] has n branches:![]()
![]()

![]() Each branch of , maps the z -plane excluding the positive real axis to the following fan-shaped regions correspondingly:
Each branch of , maps the z -plane excluding the positive real axis to the following fan-shaped regions correspondingly:
![]()
Therefore, any point on the z - plane excluding the positive real axis has n image points on the plane. At this time, assuming that the z-point at the same position on the original z - plane can be distinguished into n different points, which fall respectively On the z - plane where n leaves are cut along the positive real axis :![]()
|
|
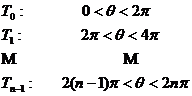
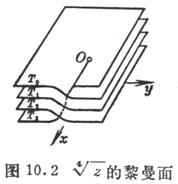
As for the points on the positive real axis, just glue the lower bank of T 0 ( ) to the upper bank of T 1 , then glue the lower bank of T 1 to the upper bank of T 2 , and finally glue the lower bank of T 1 to the upper bank of T 2. ( ) is bonded to the land ( ) of T 0 , so any point on the positive real axis can also be distinguished as a point . The plane cut by the bonded leaves along the positive real axis is called Riemann Face, Figure 10.2 is the case of n = 4 . It is single-valued on its Riemann surface .![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() is a special case where it connects the n -leaf plane . It is called a fulcrum of order n -1 , which is also an order fulcrum . The positive real axis that connects the sum of the two fulcrums is called a branch .
is a special case where it connects the n -leaf plane . It is called a fulcrum of order n -1 , which is also an order fulcrum . The positive real axis that connects the sum of the two fulcrums is called a branch .![]()
![]()
![]()
![]()
|
|
[ Riemann surface of multivalued functions ] The function has infinitely many branches:![]()
![]()
![]()
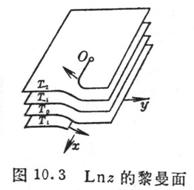
Similar to the idea of the Riemann surface, the Riemann surface is formed by bonding the z -planes cut by an infinite number of leaves along the positive real axis . Figure 10.3 is a schematic diagram of it .![]()
![]()
The function is now single-valued on its Riemann surface .![]()
![]() and are the fulcrums of infinite order .
and are the fulcrums of infinite order .![]()
![]()
In general, if the function is not single-valued in the region D , the concept of region can be generalized to make the function become single-valued in the new region . This generalized region is called the Riemann surface of the function .![]()
![]()