Chapter XII Special Functions
Special function generally refers not function solutions of certain differential equations of elementary functions can be expressed in the form of a limited , but these functions are common in applications such as Legendre functions, Bessel functions, and many orthogonal polynomials, etc. ; others is a function defined by a particular form of integration, such as ![]() - function, B . - function as well as the so-called elliptic functions from the perspective of a periodic function to consider, regardless of such functions and differential equations described in this chapter in addition to these. concept of function, but also gives some points on the function, and the infinite product series, such as expression, asymptotic form, the relationship between functions and their common properties.
- function, B . - function as well as the so-called elliptic functions from the perspective of a periodic function to consider, regardless of such functions and differential equations described in this chapter in addition to these. concept of function, but also gives some points on the function, and the infinite product series, such as expression, asymptotic form, the relationship between functions and their common properties.
This chapter references the following symbols
![]()
![]()
Where ![]() is a positive integer,
is a positive integer, ![]() an arbitrary number.
an arbitrary number.
§ 1 special functions defined by the integral
First, the
gamma function ( ![]() - function)
- function)
[ ![]() - function definitions and other expressions]
- function definitions and other expressions]
![]()
![]()
![]()
![]()
![]()
The second type is called the right of the Euler integration .
|
|
![]()
![]()
![]()
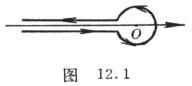
Directions from negative real axis points at infinity ![]() starting forward around the origin of the week and then return to the starting point (Figure 12.1)
starting forward around the origin of the week and then return to the starting point (Figure 12.1)
![]() Is a
Is a ![]() semi-pure function,
semi-pure function, ![]() with a single-pole, leaving the corresponding number
with a single-pole, leaving the corresponding number![]()
![]()

![]()
![]()
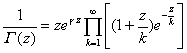
Formula ![]() called Euler's constant.
called Euler's constant.
[ ![]() function of the related formula]
function of the related formula]
![]()
![]()
![]()
![]() Is a positive integer
Is a positive integer![]()
Special
![]()
![]() (Demonstration of Odd Element style)
(Demonstration of Odd Element style)
Special
![]()
![]()
![]()
![]()
![]()
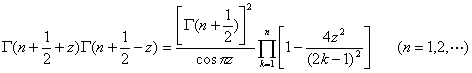
![]()
![]() (Multiplication formula)
(Multiplication formula)
![]() (Times per formula)
(Times per formula)
![]()
![]()
![]()
![]()
![]()
![]()
[ ![]() - asymptotic expression function]
- asymptotic expression function]
![]() Stirling formula
Stirling formula
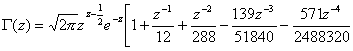
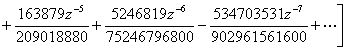
![]()
When ![]() is positive real number,
is positive real number,
(I)
![]()
Where![]()
(Ii)
![]()
![]()
![]()
![]()
The formula ![]() for Bernoulli numbers ( § 7 ) .
for Bernoulli numbers ( § 7 ) .
[Can be turned into ![]() - Function Points]
- Function Points]
![]()
![]()
![]()
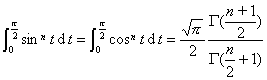
![]()
![]()
![]()
![]()
![]()
![]()
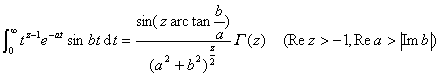
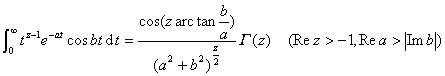
![]()
![]()
![]()
![]()